
Hypothesis testing is the number one method for researchers to test the plausibility of an assumption in statistics. However, not everyone applies this procedure correctly and sometimes data outliers, research bias or other factors can skew a distribution, making an actually wrong result appear as the right decision. These errors are called Type I and type II errors, and they will be explained thoroughly in the following article.
Definition: Type I and type II errors
The two types of errors can occur in hypothesis testing, when the null hypothesis is falsely accepted or rejected. The following graphic shows the situation visually. Type I error, also called α-error, happens when the researcher rejects the null hypothesis H0, and accepts H1, while H0 is actually correct. Type II error, or β-error, on the other hand, describes the case where H0 is accepted as right, while the population would actually represent H1.
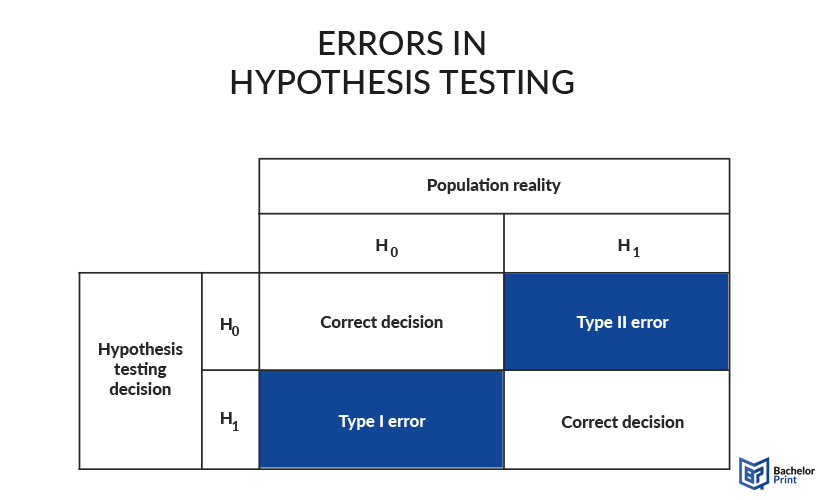
In research, the null hypothesis is defined as H0, which assumes no effect on the test subjects. H1, on the other hand, also called alternative hypothesis, always states the researcher’s assumption of the effect. Depending on the type of hypothesis statement, H0 can also represent every other possible outcome than the one stated in the alternative hypothesis.
Type I and type II errors explained
Understanding the relationship between variables in a test scenario helps to identify the likelihood of type I and type II errors. Statistical methods use estimates in making assumptions which may result in type I and type II errors from a flaw in data collection and formulation of assumptions as follows:
Type I errors – False positives
A type I error refers to the situation where a researcher implies that the test results are caused by a true effect when they are caused by chance. The significance level is the likelihood of making a type I error. The significance level is often capped at 5% or 0.05. This means that if the null hypothesis proposed is true, then the test results have a 5% likelihood of happening or less. The initial p-value determines the statistical chances of arriving at your results.
Type II Errors – False negatives
A type II error occurs when the null hypothesis is false, yet it is not rejected. Hypothesis testing only dictates if you should reject the null hypothesis, and therefore not rejecting it does not necessarily mean accepting it. Often, a test may fail to detect a small effect because of low statistical power. The statistical power and a type II error risk have an inverse relationship. High statistical power of 80% and above minimizes the type II error risk.
Consequences
While both types of errors are equally bad for the study, type I errors are usually worse. This is due to the fact that rejecting an actually valid null hypothesis results in the assumption, that the actual thesis is correct. In medical context, this can mean that a treatment is assumed to be effective, leading to high investments into further studies and application of the drug. However, the medicine does not even have an effect, resulting in a huge waste of money.
Type II errors, on the other hand, merely result in missed opportunities. While this is unfortunate and may have consequences for the researchers as well, it is less likely to cause financial and reputation losses.
The consequences of type I and type II errors include:
- Wastage of valuable resources.
- Creation of policies that fail to address root causes.
- In medical research, leads to misdiagnosis and mistreatment of a condition.
- Fail to consider other alternatives that may produce a better overall result.
Avoiding errors
Individually, the chance for type I errors can be decreased by decreasing the significance level. Usually, this is set to 5%, but a decrease to 1% highly lowers the risk of type I errors to 1%. Type II errors, on the other hand, can be mainly avoided by increasing the statistical power of the study, e.g., through decreasing the standard error. Generally, the probability of one type can be decreased by measures that increase the probability of the other one. A universal approach to avoid type I and type II errors in hypothesis testing is always to increase the sample size. The more participants a study has, the greater is the statistical power and the lower is the risk of accepting the wrong conclusion.
Printing Your Thesis With BachelorPrint
- High-quality bindings with customizable embossing
- 3D live preview to check your work before ordering
- Free express delivery
Configure your binding now!
FAQs
Type I and type II errors are wrong conclusions in hypothesis testing. Type I falsely rejects the null hypothesis, while type II falsely accepts it.
The simplest method is to increase the sample size of your study. A larger sample size automatically means a higher validity and thus decreases the chance for any errors. Individually, the chance for type I error can be reduced by decreasing the significance level, while type II errors can be reduced by decreasing the standard error.
Although both types of errors should be avoided in any study, type I error is worse when it comes to practical application. This is the case because a type I error means that a treatment, that has been tested on its efficiency, is assumed to be working while it actually does not. Investments will be made to support further development and a lot of money will be lost. Type II error merely equals a missed chance.
