Statistical tests are an integral part of academic writing, particularly in research that involves data analysis. These tests, from t-tests to chi-square, ANOVA, or regression analysis, provide a structured way to interpret data, helping to confirm or reject hypotheses. A hypothesis refers to a phenomenon or scientific observation to be tested further using statistical tests. Statistical tests are used in probability research. They are used by researchers to confirm whether a data set sufficiently supports the hypothesis of the study.
Statistical Test – In a Nutshell
- Statistical sets are an essential tool in research.
- They are used to test the differences between variables in a data set to determine causality and correlation.
- There are different types of statistical sets for the various types of data used for research.
Definition: Statistical tests
Statistics is the science of gathering, organizing, summarizing, and analyzing data in the interest of a research problem. Statistical tests are one of the tools used to assert if an input variable has a statistical effect on a resultant variable. They are also deployed to determine the difference between two or more classes.
Statistical tests further assume the null hypothesis, which states that there are no differences between two populations or classes. Two possibilities are the same, and any significant, observable differences are purely by chance or error.
Purpose of statistical tests
Statistical tests begin by estimating a test statistic. The test statistic measures the variation between the variables in a test and the null hypothesis, where no differences exist.
Statisticians then calculate the p-value. It is a statistical measurement that compares a proposed hypothesis with observable characteristics in the data set.
The p-value estimates the likelihood of arriving at the observable outcomes if the null hypothesis is true.
A less extreme difference between the test and null hypothesis statistic implies no significant relationship between the input and outcome variables.
On the other hand, if the difference is more extreme, the conclusion is a statistically significant relationship between the input and outcome variables.
Performing statistical tests
Statistical tests require a large sample size to determine the accurate distribution in the population postulated for research. Data for statistical tests can be collected from experiments or probability samples obtained from observations.
Researchers may use different types of statistical tests depending on:
- How the data meets defined assumptions
- The types of variables present
Statistical Assumptions
Statistical tests assume the following conditions:
| No autocorrelation/Independent observations | The variables in the test should not be related; for instance, different test subjects are independent. The observations in one sample should be different from the next. |
| Homogeneity of variances | In a test case, the variance within one group should be similar across other groups. Variations in variances reduce the accuracy of a statistical test. |
| Normality | The data in a quantitative statistical test should exhibit the pattern of a normal distribution curve.5 |
However, you may encounter data sets that fail to meet one or more of these assumptions. You can perform other tests in this case.
For instance, nonparametric statistical tests are used when there is no homogeneity or normality in the data. Repeated measured tests can be conducted where the data lacks independent variables.
Types of variables
Different statistical tests are best suited for different types of variables. Some of the variables include:
Quantitative variables
These are numerically measurable variables, such as the number of cars in a lot.
Quantitative variables can be further classified into:
- Continuous variables: Also known as ratio variables. These are units of measurement that can be represented in quantities less than 1. For instance, 0.8 km.
- Discrete or integer variables: Units that cannot be divided, such as 1 car or 1 tree.
Categorical variables
They describe classes or groups of things, for instance, the models of a vehicle.
Categorical variables are divided into the following variables:
- Binary: Data that has one of two outcomes, such as yes/no or pass/fail
- Nominal: Used to describe data with no intrinsic order, such as brands, families, species
- Ordinal: For ordered data types with observable scales of hierarchy, such as user ratings.
Statistical tests: Parametric test
Parametric tests are used in samples that exhibit a normal distribution, among other statistical assumptions. They use these assumptions to control the sample distribution to achieve stronger conclusions compared to nonparametric tests.
Parametric tests include:
Regression tests
They measure the relationship between two variables for causality and effect. Regression tests in statistical contexts include simple linear, multiple linear, and logistic regressions.
Comparison tests
These tests evaluate the difference between group averages. They determine the effect of a given variable on the mean value of other variables.
- Used to compare the averages in two groups, for instance, the mean age of boys and girls in a class.
- A statistical test to determine statistical differences in the mean of more than two independent groups.
MANOVA
- It is used where there is more than one variable used to determine the mean differences in three or more independent groups.
Example t-test
- What is the difference in terms of the final grade point average for students from two different schools?
Example ANOVA
- What is the difference in average speed among drivers given three different car makes?
Example MANOVA
- What is the effect of pop culture on behavior, social skills, and personality?
Correlation tests
Correlation tests determine the relationship between two variables without proposing a cause-effect relationship. They can be used in multiple regression to test if there is autocorrelation between two variables.
Example
How are temperature and rainfall related?
Statistical tests: Nonparametric test
Nonparametric tests don’t require any underlying assumptions in the research data. They are applied when a sample fails to follow acceptable statistic assumptions.
Nonparametric tests are, however, not considered as strong as parametric evaluations.
Types of nonparametric tests:
- Spearman’s r
- Chi-square test of independence
- Sign test
- Kruskal-Wallis H
- ANOSIM
- Wilcoxon rank-sum test
- Wilcoxon signed-rank test
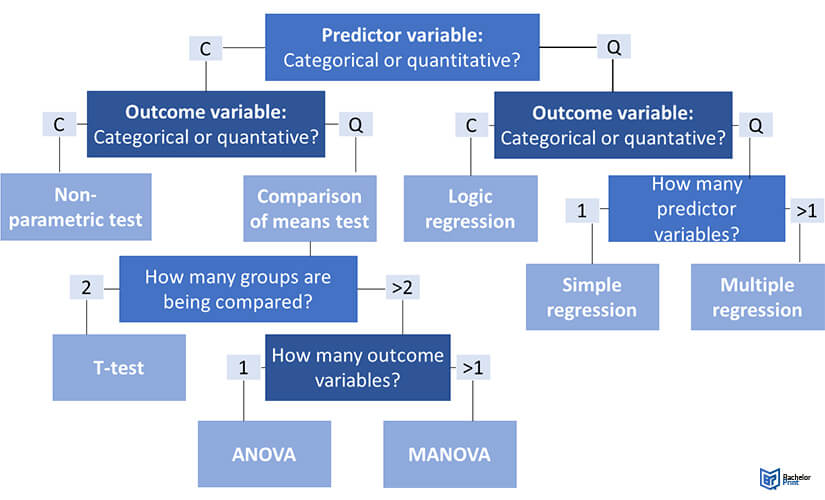
Choosing a statistical test: Flowchart
The following flowchart allows you to choose the correct statistical test for your research easily.
Printing Your Thesis With BachelorPrint
- High-quality bindings with customizable embossing
- 3D live preview to check your work before ordering
- Free express delivery
Configure your binding now!
FAQs
A test statistic is a unit or quantity calculated from a sample in research. Test statistics are used as an evaluative metric in analysis for hypothesis testing.
Statistical tests are used to test and determine the differences between two variables, i.e., the predictive and output variables in a study. The tests always assume a null hypothesis between two samples.
Parametric tests are where there are observable statistical distributions in a data set. Nonparametric tests do not consider any distributions and do not consider statistical assumptions.
Statistical tests are applied to study research problems with several variables. Researchers do statistical tests to see how different variables interact and how much they affect each other.
The statistical assumptions used in statistical tests are independent observations, normality, and homogeneity. Nonparametric tests are used if one or more of these conditions is missing in a data sample.
