The best and most common method for measuring a linear correlation is calculating the Pearson correlation coefficient. This approach in statistics provides a significant formula in the field of experimental research. This article will account for the various types, how to calculate them, and the significant test. Furthermore, this guide will provide an in-depth understanding of using this method and give respective examples for visualization and clarity.
Inhaltsverzeichnis
Pearson Correlation Coefficient – In a Nutshell
- The Pearson correlation coefficient is an expressive statistic that measures the strength between diverse variables and how they relate.
- In simpler terms, the Pearson correlation coefficient recaps the features of a dataset.
- This article gives insight into the various types of Pearson correlation coefficients
- It also outlines the steps of how to calculate the Pearson correlation coefficient.
Definition: Pearson correlation coefficient
The Pearson correlation coefficient is an expressive statistic that measures the strength between diverse variables and how they relate. In simpler terms, it recaps the features of a dataset. The Pearson correlation coefficient is also known as:
- Bivariate correlation
- The correlation coefficient
- Pearson’s r
- (PPMCC) Pearson product-moment correlation coefficient
Types of Pearson correlation coefficients
The Pearson correlation coefficient is a digit between -1 and 1 that calculates the strength and course of the affiliation between two variables. The table below provides a vivid explanation.
| Pearson correlation coefficient (r) | Correlation type | Interpretation | Example |
| Between 0 and 1 | Positive correlation | A change in one variable triggers a change in the other in the same direction | Height and weight of a person: The taller a person gets, the heavier they weigh |
| 0 | No correlation | The variables are not affiliated | Cost of shoes and width of cars: The price of shoes will not influence the width of your cars and vice versa. |
| Between 0 and -1 | Negative correlation | A change in one variable triggers a change in the other in the opposite direction | Elevation and temperature: The higher you go, the lower the temperature |
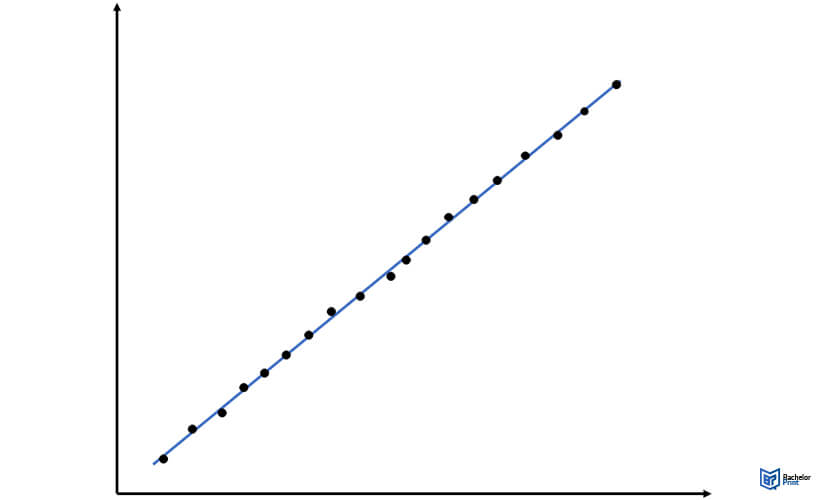
Positive correlation
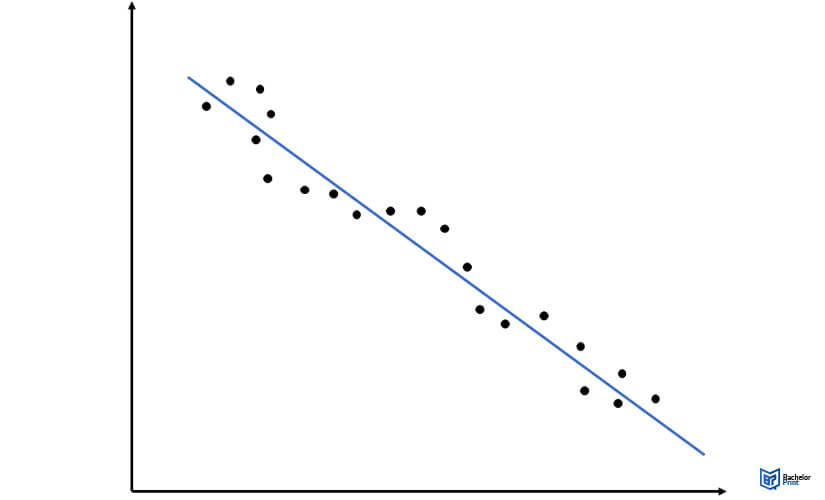
Negative correlation
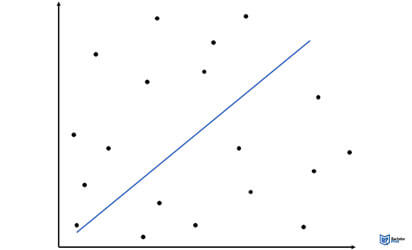
No correlation
The effect size (relationship strength) interpretation may vary depending on the discipline. However, the following standard rules still apply.
| Pearson correlation coefficient (r) value | Strength | Direction |
| Higher than .5 | Strong | Positive |
| .3 to .5 | Moderate | Positive |
| 0 to .3 | Weak | Positive |
| 0 | None | None |
| 0 to -.3 | Weak | Negative |
| -.3 to -.5 | Moderate | Negative |
| Below -.5 | Strong | Negative3 |
Besides descriptive statistics, the Pearson correlation coefficient can also be used for testing statistical hypotheses because it is an inferential statistic.
Visualizing the Pearson correlation coefficient
You can visualize Pearson’s r as a measure of how close the observations in experimental research are to a line of best fit. Also, it tells you whether the slope of the line of best fit is positive or negative.
Example
The line of best fit is when r is 1 or -1.
Pearson correlation coefficient vs. Spearman’s rank correlation coefficients
Besides the Pearson correlation coefficient, another popular correlation coefficient is Spearman’s rank correlation coefficient.
It is a go-to method when at least one of the following characteristics is true:
- The variables are ordinal
- The variables are not distributed normally
- The data features outliers
- The variables have a non-linear or monotone relationship
Calculating the Pearson correlation coefficient
While the formula is easy to use, you can apply software tools like R or Excel to help you calculate the Pearson correlation coefficient.
Example
You are researching the relationship between the weight and length of newborn babies and have data from 10 babies born within the last four weeks at a local clinic. After translating the imperial dimensions to metrics, you enter the data in this table:
| Weight (kg) | Length (cm) |
| 3.33 | 52.9 |
| 3.63 | 53.2 |
| 3.02 | 49.7 |
| 3.82 | 48.4 |
| 3.59 | 54.9 |
| 3.42 | 54.2 |
| 2.87 | 43.7 |
| 3.36 | 54.4 |
| 3.03 | 47.2 |
| 3.46 | 45.2 |
Pearson correlation coefficient in a thesis
The Pearson correlation coefficient usually comes up in the results section of an academic paper or thesis. Apply the rules below if you want to report in APA style:
- No need for a reference
- Italicize r
- Include a leading zero before the decimal point
- Provide two significant digits after the decimal point
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing
FAQs
You should use this method in inferential statistics or quantitative statistics. You can also use it to test correlations between two variants.
It helps test the relationship between two variants. It also helps determine the course of change if either variant is altered.
It isn’t easy to calculate. However, if you master the formula, you should be okay.
