Statistical tests, especially hypothesis testing, requires stating hypotheses and seeking to prove or reject them. This procedure is significant during your thesis writing too because in this academic work, you seek to answer your research question by evaluating your study. Before you can conduct your research, you first have to set the two main hypotheses: the null hypothesis and the alternative hypothesis. This article will teach you everything you need to know about these two, along with various examples.
Definition: Null and alternative hypotheses
The null and alternative hypothesis, in statistics, are complementary, meaning that once you set one of them, the other one has to cover every other possible outcome of the study. Typically, the null hypothesis (H0) expects no effect, no change, no difference, while the alternative hypothesis (H1 or Ha) states the expectation of the researcher and the result they want to have.
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing

Differences
Both hypotheses provide possible but mutually exclusive answers to a research question. They can only be rejected or supported through statistical testing.
The differences between them are:
| Null hypothesis (H0) | Alternative hypothesis (Ha) |
| Claims there’s no relationship between variables. | Claims there is a relationship between variables. |
| Common expressions used to write it include no relationship, no effect, no difference, no increase, no decrease, and no change. | Common expressions used to write it include a relationship, an effect, a difference, an increase, a decrease, and a change. |
| If testing shows there’s a relationship, this is reported as p ≤ α, therefore H0 is rejected. | If testing shows there’s a relationship, this is reported as p ≤ α, therefore Ha is supported. |
| If testing shows there’s no relationship, this is reported as p > α, therefore we fail to reject H0. | If testing shows no relationship, this is reported as |
One-tailed vs. two-tailed test
Hypotheses can be differentiated by whether they conduct a one-tailed test or a two-tailed test. One tailed means that the alternative hypothesis covers one side of the spectrum, while the null hypothesis covers the second half. The important thing is that the threshold always needs to be included in one of the hypotheses, as seen below.
A two-tailed test, on the other hand, asks for a specific value or range, while the null hypothesis covers both ends of the surrounding spectrum.
Hypothesis testing
Hypothesis testing is the procedure to determine which of the two hypotheses is the most plausible one. Generally, you reject the null hypothesis when p > α. To find out more about how hypothesis testing works and which tests you can use, have a look at our article on that topic.
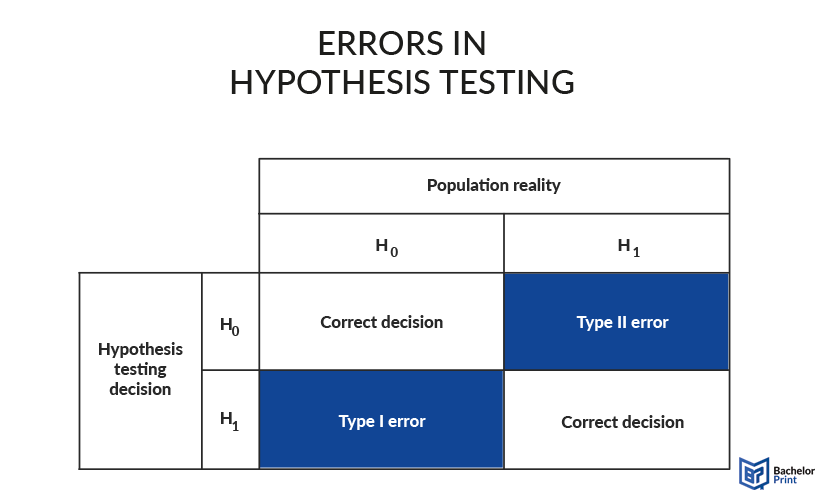
Type I and Type II errors
While conducting hypothesis testing, there are two essential errors, which can occur. They are called Type I and Type II errors, or also ɑ-error and β-error. These mistakes happen when the wrong hypothesis is assumed to be right. Type I refers to when the null hypothesis is rejected, although it should have been accepted. Type II refers to the case when the null hypothesis is accepted, although it should have been rejected. The following image will show you the differences visually.
Examples
The following examples will provide you with insight on how to phrase null and alternative hypotheses in various contexts.
Research questions
These hypotheses function as tentative answers to research questions. Therefore, you can’t have an answer to your research question without confirming or rejecting either hypothesis.
Both hypotheses are tested using statistical tests that compare two population samples/groups. Testing confirms or rejects the hypotheses, by showing whether there’s a relationship between an independent variable and a dependent variable.
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing

FAQs
Hypotheses are unproven statements about a research question. The null hypothesis says there is a relationship between variables, and the alternative hypothesis claims there isn’t one.
No, these hypotheses are competing statements, so when you test one hypothesis, you automatically test the other. That said, you should not try to work with two alternative hypotheses, as testing them at the same time is not possible.
For testing hypotheses, you can use t-tests, ANOVAs, linear regression, corelation coefficients and many other statistical tests depending on your hypotheses, samples and overall study design.
