Conducting a study for statistics can be elaborate, and often there is no time to redo a study if the results are unsatisfying or warped. This is why, before you start your study, you should get to know different types of research bias to avoid. Another dangerous encounter in datasets after collection are outliers. They are extreme values that can alternate the result of any statistical analysis. The following article will teach everything you need to know about data outliers and how to work with them.
Data Outliers in a nutshell
Data outliers are extreme values in a dataset, that differ greatly not only from the mean, but also from the other values. They can interfere with the statistics of your study and influence the result in a negative way.
Definition: Data outliers
Data outliers are values that differ significantly from the rest of the dataset. They represent information on out-of-the-ordinary behaviour, such as numbers far from the norm for the variable in question. Depending on the overall context of the data, outliers can signify an error in data collection or measurement or interesting anomalies such as rare occurrences or extreme values.
Data outliers are problematic in statistics because they:
- Affect the accuracy of estimates and even cause bias
- Skew the average if they aren’t distributed randomly
- Affect the validity of statistical hypotheses like regression
- Make statistical tests less predictive when error variance increases
Example
In a dataset of test scores for a class, an outlier could be an extreme 98% score when the rest of the scores range from 60% to 80%. This outlier could be due to various factors, such as cheating, a mistake in grading or a highly intelligent student. If this outlier is not identified and dealt with, it could skew the overall average score for the class, leading to incorrect conclusions or decisions based on the data.
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing
Different types of data outliers
There are various data outliers, but broadly speaking, they can be categorized into three types:
Global, Contextual, and Collective
These are the most basic kind of data outliers. They are data points that are significantly different from other points in the dataset.
These types of data outliers can occur due to measurement errors or represent extreme values in the population. Existing outlier detection methods often focus on finding global outliers.
These data points are not considered when in isolation but become outliers when context is considered.
Example
A high temperature reading on a hot summer day may not be an outlier on its own, but it would be considered an outlier on a cold winter day.
Without relevant background information, it can be challenging to identify contextual outliers in a given set of data. For this reason, it is essential to have a description of the context at hand.
These are groups of data points that are significantly different from the other groups in the dataset. These types of data outliers can occur when there are subgroups or clusters of data with different characteristics or errors in the grouping or categorization of data.
Finding data outliers
Detecting data outliers is essential in data analysis as it ensures data quality, statistical significance, and accurate modelling . There are several techniques for finding them, each of which takes a different approach.
Sorting data
Sorting your data is an easy way to identify outliers because it allows you to see the extreme values at a glance. You can sort your data in ascending or descending order, depending on the variable of interest, and then check for abnormally high or low values.
Example
If you are analysing a dataset of exam scores: 78, 85, 92, 67, 88, 99, 76, 25, 84, 92, sorting the data would look like 25, 67, 76, 78, 84, 85, 88, 92, 92, 99.
In this case, you can easily spot that the score of 25 is an outlier.
Graphing data
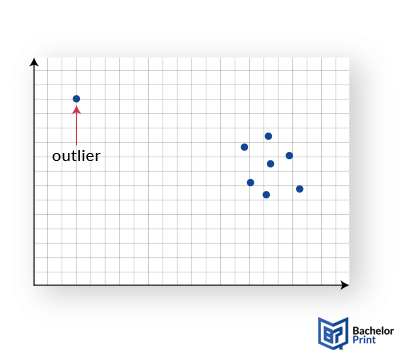
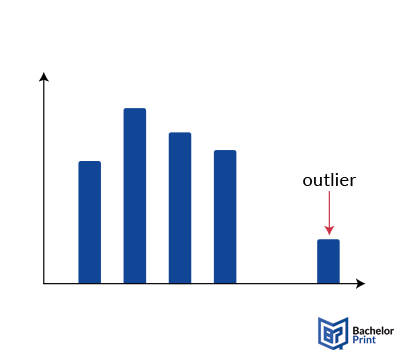
Graphs like scatter plots and histograms can also be used to identify data outliers. Graphs provide a visual representation of your data, making it simple to highlight patterns and spot outliers.
Outliers will manifest as points that display a notable deviation from the rest of the dataset. A scatter plot displays data points as dots on an x-y graph, depending on two variables. Since most points tend to cluster together, scatter plots make it simple to spot outliers. The extreme number is the outlier.
In contrast, histograms use bars to organize data. The data ranges are shown along the x-axis, while the other variable is along the y-axis. This helps in locating outliers in the data. For example, if most data points autumn on the right-hand side of the graph, a small bar on the left stands out as an anomaly.
Z-scores
A Z-score represents the number of standard deviations a data point differs from the mean of a dataset. Z-scores are obtained by taking a data point, subtracting the mean, and then dividing by the standard deviation.
The formula for calculating a z-score is:
z = (X – μ) / σ
Where:
- z = z-score
- x = data point
- μ = mean of the dataset
- σ = standard deviation of the dataset
If the Z-score for any of the data points is significantly greater or lower than 0, then that data point can be considered an outlier.
Example
If your data points have z-scores of -0.32, -0.15, -5.2, -0.29, and -0.19, respectively, the one with a z-score of -5.2 stands out as the outlier.
Interquartile range
The interquartile range (IQR) is a measure of variability that tells how spread out the middle 50% of the dataset is. To identify data outliers using the IQR method, a general rule is to consider any data point that falls more than 1.5 times the IQR below the first quartile or above the third quartile as an outlier.
Q1 and Q3 denote the first and third quartiles of a dataset and the quantitative difference between the upper and lower quartiles of the dataset.
Tukey method
The Tukey method, also known as the Tukey fence method, is a variation of the IQR method that uses fences to identify data outliers.
A fence is a threshold value beyond which any data point is considered an outlier. The fences are calculated by adding or subtracting a multiple of the IQR from the first and third quartiles. Any data point that falls outside of the fences is considered an outlier.
The fences are calculated as follows:
- Lower fence = Q1 – (1.5 x IQR)
- Upper fence = Q3 + (1.5 x IQR)
Standard deviation
The standard deviation can also be used to determine outliers. Usually, you would calculate the mean and then the standard deviation. Then you divide the dataset into three groups: one that is one standard deviation added or subtracted from the mean, these are the typical values. Two standard deviations around are untypical, and everything outside the two standard deviation radius can be considered an outlier.
Dealing with data outliers
After the identification of outliers in your dataset, the next question is how to deal with them. Outliers can heavily affect your data analysis and thus need to be carefully considered. While occasionally, it can be beneficial to simply remove them, it is technically a form of research bias, which should be avoided if possible.
Removing
The simplest method to deal with any data outliers is removing them. Therefore, you use the abovementioned methods to detect outliers and either remove all of them or just the outermost values. While this is technically knowingly induced research bias, sometimes it can be helpful, as outliers easily skew a distribution to an extent, that it does not represent the population accordingly anymore. Especially when the origin of the outliers might lie in sampling mistakes, it is clever to just remove the outliers.
Transformation
Transforming the entire dataset with mathematical operations can also help to minimize the impact of outliers on the distribution. Popular methods are using logarithms for right skewed data or the square root for huge outlier values.
Replacement
Outliers can also be dealt with by replacing them with other values. These can be estimated through the rest of the dataset. One way to do this is by replacing outliers with the mean or median, while others use linear regression to approximate a new value.
Segmentation
If there is not just one or two outlier values, but an entire group of them, it might be beneficial to separate these groups and analyse them individually. This way, it is possible to find new patterns and subgroups of the population, that may need further investigation.
Robust methods
A different method, used when the outliers are completely valid and potentially necessary in the distribution, is to take advantage of statistical procedures that minimize their impact. The median, for example, is not influenced by outliers, as well as some regression-based models. Especially when it comes to measures of central tendency, it is essential to know which ones are affected by outliers and which one are not, which is described in the corresponding article.
True and false data outliers
Data outliers can occur due to different reasons, and it’s important to distinguish between true outliers resulting from natural variation in a population and outliers arising from measurement errors or incorrect data entry.
Outliers resulting from natural variation in the population are referred to as true/real outliers. These data outliers can provide valuable insights into the data distribution and the population’s characteristics under study.
Example
If you have a dataset on the heights of people in a population, a true outlier could be the height of an exceptionally tall person, which would reflect the natural variation in the height of the population.
In contrast, data outliers arising from measurement errors or incorrect data entry are known as false/spurious outliers. These can distort the distribution of the data and can result in incorrect conclusions or analyses.
Example
If you have a dataset on the weights of individuals, an extremely high recorded weight due to a measurement or data entry error is a spurious outlier, which is not caused by the participant.
When dealing with many outliers or a skewed distribution, it’s essential to consider what caused them.
If the outliers are due to measurement errors or incorrect data entry, they should be corrected or removed from the dataset.
However, if the outliers are due to natural variation in the population, they should be retained in the dataset.
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing
FAQs
Data outliers are not always bad, but they can indicate errors or unusual patterns in the data that may warrant further investigation.
Preventing outliers in data can be challenging, but some measures can be taken, such as high data quality through random sampling, appropriate measurement techniques and skilled personnel for conducting the study or setting realistic thresholds for data values.
For skewed datasets, the best method for removing the outliers is the IQR method. However, if the data is normally distributed, which is often the case, it’s best to use the standard deviation.
