
Variability is a statistical unit that is used to create conclusions from a data set. It is used by researchers and statisticians in several fields to make deductive assertions through a series of tests.In descriptive statistics refers to the spread or dispersion of data points around a central tendency. Measures of variability, such as range, interquartile range, variance, and standard deviation, help us understand the spread of data. This article delves into the various measures with examples.
Definition: Variability
In statistics, variability is the extent to which data in a data set varies. It shows how much the elements in a data group differ by metrics such as size.
The most common methods of measuring variability are:
- Range – The difference between the highest and the lowest value in a data set, the average of the two is known as the midrange.
- Interquartile range – The middle range of your ordered data, the difference between the third and first quartile.
- Standard deviation – The dispersion of data values from the group’s nasty, derived as the square root of the variance.
- Variance – It quantifies the average squared deviation of individual data points from the nasty, calculates the difference between the dataset and average.
Why is variability important
Data sets that display low variability can design predictive models, as they are reasonably consistent. High variability scenarios are hard to predict due to their wide dispersion.
Data groups may have the same central tendency but exhibit different variability. Thus, variability supplements central tendency and other statistical measures to give a stronger summary of the conclusions from a test.
Measuring variability: Range
It is the difference between the largest and the smallest value. The formula for the range is expressed as:
Range (R) = Highest number (H) – Lowest number (L)
Calculating the statistical range of data gives a relatively accurate measure of variability. However, outliers in the data group may give misleading conclusions. Outliers refer to extreme values that are dissimilar from other values in a group.
The last value is an outlier. Outliers can affect deductions from the range because the range only considers two numbers, i.e., the largest and the smallest. The ranges should therefore be applied alongside other measures.
Range calculation example
If you have 6 data elements from a sample:
Measuring variability: Interquartile range
The interquartile range (IQR) is the range of the middle values in an ordered data set. Quartiles are used in descriptive statistics to divide an ordered data group into four equal parts.
Interquartile range calculation example
The interquartile range is calculated as follows using a previous day’s data set:
Q1 can be expressed as the 2nd element which is 25 while Q3 is the 5th element which is 45
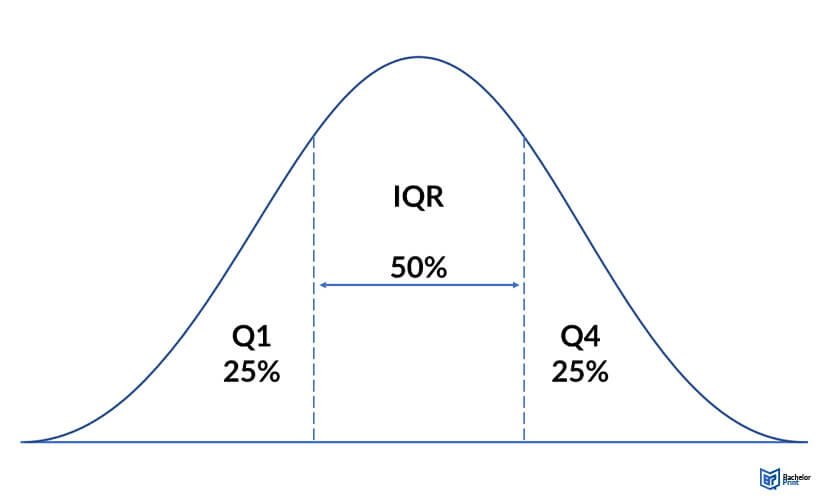
Measuring variability: Standard deviation
The standard deviation is the nasty of the variability in a data group.
Calculating standard deviation involves six steps:
- Outline every score and calculate the nasty.
- Deduct the value of the nasty from each score to find the deviation.
- Find the square of each deviation.
- Find the sum of the squared deviations.
- Divide the total squared deviations by n-1.
- Calculate the square root of each result.
Standard deviation with a sample
Data samples are subsets of data groups derived from the selection and analysis of patterns in a population. The standard deviation of a sample is calculated from the following formula:
| Formula | Explanation |
| The standard deviation of the sample | |
| The sum of | |
| Each value | |
| Mean of the sample | |
| Number of units in the sample |
Standard deviation calculation example
From the data set proposed:
Standard deviation with a population
A statistical population in descriptive statistics refers to the pool of individuals or objects that a researcher is interested in. The standard deviation of a population is calculated as follows:
| Formula | Explanation |
| Standard deviation | |
| Sum of | |
| Each unit | |
| Mean of the population | |
| Values in the population |
Measuring variability: Variance
Variance is the nasty of the squared deviations from the average of the data group. It is derived by squaring the standard deviation.
Variance with a sample
The following formula is used to calculate the variance of a sample:
| Function | Explanation |
| Variance of the sample | |
| Sum of | |
| Each value | |
| Mean of sample | |
| Number of values |
Variance calculation example
From our previous data set:
Variance with a population
You can also determine the variance of a population. The formula for finding the variance of a population is:
| Formula | Explanation |
| Population variance |
|
| Sum of | |
| Each value |
|
| Mean of population | |
| Number of values present |
Determining the best measure of variability
The distribution and level of measurement dictate the most suitable measure.
Level of measurement:
- The range and interquartile measures are preferable for ordinal measurements. Standard deviation and variance are used for sophisticated ratio measurements.
Distribution:
- All the measurement types can be applied for normal distributions.
- Variance and standard deviation are used often because they consider every element of a data group.
- However, this also makes them highly susceptible to outliers.
- For data groups with outliers such as skewed distributions, it is best to use the interquartile range as it focuses on the dispersion in the middle.
- ✓ 3D live preview of your individual configuration
- ✓ Free express delivery for every single purchase
- ✓ Top-notch bindings with customised embossing

FAQs
The range – the easiest measurement level is derived from the difference between the smallest and largest values in a data set.
- Standard deviation measures the spread of values from the nasty.
- Variance is the square of standard deviation.
An example is observed in production lines. Specifications are made using computers to produce identical parts, but there are still anomalies. Variance and other measures of variability estimate the deviations from the desired nasty.
A biased estimate gives consistently high or low results. It has a systematic bias that emphasizes consistent values.
